Om konvergens av talföljder
advertisement

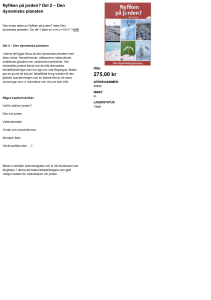
Arbetsblad 5 (MATLAB) Anders Källén Om talföljders konvergens Introduktion I det här arbetsbladet ska vi diskutera olika sorters oändliga talföljder. Den viktiga frågan vi ska adressera är om den konvergerar mot något visst tal, går mot oändligheten eller bara uppför sig väldigt oregelbundet. Idén är att vi ska experimentera i MATLAB för att gissa vad som gäller, men också hitta metoder att matematiskt verkligen visa att det händer som vi tror händer. 1.6 3 1.4 2.5 för någon funktion f ( x ) av en variabel, kallas relationen ett dynamiskt system i diskret tid. Om vi bestämmer ett startvärde a0 så definierar detta en oändlig talföljd, vilken kallas lösningen till det dynamiska systemet. 0.6 0.4 0.5 0 1 6 7 8 9 Beskriv sedan vad som händer med an då n → ∞ (n växer obegränsat). Svaret beror på r! 10 11 12 Om du har tänkt rätt på övningen vet du att (1) 14 15 16 17 Definition Den matematiska definitionen av (1) är att det till varje e > 0 ska finnas ett heltal N sådant att om n > N så gäller att | an | < e, dvs n > N ⇒ | an | < e. 18 19 2 3 0 4 0 5 10 15 20 r =0.5; b=1; f =@( x ) r ∗x+b ; N= 2 0 ; a0 = 0 . 1 ; A=a0 ; f o r i = 1 :N−1 a1= f ( a0 ) ; A = [A a1 ] ; a0=a1 ; end 21 23 Vi får sedan att lim ( an − A) = 0. n→∞ En enkel rekursionsmodell Det kanske näst enklaste dynamiska system tar f ( x ) = rx + a där r, a är olika reella tal, alltså subplot ( 1 , 2 , 1 ) f p l o t (@( x ) [ f ( x ) , x ] , [ 0 , 4 , 0 , 4 ] ) ; l i n e (A( [ 1 1 2 ] ) , [ 0 A( [ 2 2 ] ) ] ) ; f o r i = 2 :N−1 l i n e (A( [ i i i + 1 ] ) ,A( [ i i +1 i + 1 ] ) ) ; end 20 22 an+1 = ran + b, 1 13 om |r | < 1. Men vad betyder detta? ⇔ 0 Matlab-koden som skapat detta är: 5 lim an = A 0.2 4 där r är ett reellt tal. Visa att lösningen på det består av den geometriska talföljden an = ar n . n→∞ 0.8 1 3 a0 = a, 1 1.5 2 Övning Det enklaste exemplet på ett dynamiskt system är lim an = 0 1.2 2 Talföljder kan uppkomma på många olika sätt. Om det är så att det n:te talet an bestäms helt av det föregående, säger man att talföljden är rekursivt bestämd. Har man en matematisk relation (formel) kallas denna en rekursionsformel för talföljden. Om an+1 bestäms ur an genom en formel a n +1 = f ( a n ) an+1 = ran , 1.8 3.5 Dynamiska system i diskret tid och en variabel n→∞ 2 4 subplot ( 1 , 2 , 2 ) p l o t ( 1 : N, A, ’ o ’ ) ; Notera här att vi infört kommandot subplot så att vi får två fönster bredvid varandra. Kommandot är subplot(n,m,k) (inget semikolon!) delar in grafikfönstret n × m delfönster och k talar om i vilket fönster vi just nu ritar. I figuren ser vi att an kommer närmare och närmare skärningspunkten mellan de två graferna, alltså lösningen på ekvationen f ( x ) = x. Denna lösning är a0 = a. Detta kan vi lösa (se övning längre ner), men vi gör inte det nu. Istället ska vi förstå vad som händer då n → ∞ genom att rita in de två graferna y = f ( x ) och y = x i samma figur. Rita nu in talet a0 på x-axeln. För att få a1 = f ( a0 ) geometriskt går vi upp parallellt med y-axeln från a0 på x-axeln till grafen för f och därefter parallellt med x-axeln till linjen y = x. Om vi nu går ner till x-axeln parallellt med yaxeln hamnar vi i punkten a1 . För att få a2 = f ( a1 ) förfar vi på samma sätt igen utifrån a1 . Vi fortsätter sedan denna process. För att se vad som händer låter vi MATLAB rita upp detta åt oss. I figuren nedan har vi till vänster ritat in den beskrivna processen och till höger har vi plottat an mot n för de speciella valen r = 0.5 och a = 1. a∗ = b 1−r och vi tror oss alltså förstå att an → a∗ då n → ∞. Övning Experimentera med andra r och andra startvärden. För vilka r verkar du få detta resultat (att talföljden närmar sig skärningen mellan de två kurvorna) och vad händer för andra tal. Försök att göra en så noggrann utredning som möjligt genom att variera r (spelar b någon roll?). Vi ska nu se matematiskt vad som händer. Vi gör det i steg: 1. Sätt cn = an − a∗ . Då löser cn rekursionsformeln cn+1 = rcn och är alltså en geometrisk serie: cn = ( a0 − a)r n . 2. Då |r | < 1 gäller att cn → 0 då n → ∞, vilket betyder att lim an = a∗ En kul datorövning som ansluter till diskussionen ovan är att studera det dynamiska systemet an+1 = (1 + r ) an − ra2n n→∞ i det fallet. 3. Då r ≥ 1 gäller att cn → ∞ då n → ∞, varför detta även gäller an . 4. Då r < −1 gäller att cn svänger mellan positiva och negativa värden, men |cn | → ∞ då n → ∞, varför detta även gäller an . 5. Slutligen, då r = −1 har vi att an = − an−1 + b = −(− an−2 + b) + b = an−2 , så a0 = a2 = a4 = a6 = . . .. På samma sätt gäller att a1 = a3 = . . . = b − a0 . Lösningen bstår alltså av två värden, a0 och a1 = f ( a0 ). En sådan lösning kallas en 2-cykel. Övning Vi har också en explicit lösning här: a n = r n a 0 + b (1 + r + . . . + r n −1 ) = r n a 0 + b På väg mot kaos 1 − rn . 1−r Bevisa det och härled resultatet ovan från denna formel istället. Några icke-linjära modeller Samma idé som ovan kan tillämpas på mer komplicerade modeller. Gör följande övningar grafiskt i MATLAB först och försök sedan bevisa det du ser matematiskt. I det här avsnittet betraktar vi bara system med positiva startvärden a0 . Övning Betrakta det dynamiska system som fås med hjälp av funktionen bx . f (x) = 1+x Studera lösningarna till detta dynamiska system för olika startvärden a0 . Är följande hypotes rimlig från dina simuleringar: 1. Om b ≤ 1 gäller att an → 0 då n → ∞, 2. Om b > 1 gäller att an → (b − 1) då n → ∞? Försök sedan bevisa påståendet matematiskt. Ett sätt att göra det är att betrakta cn = 1/an (men detta är speciellt för detta problem). Lösningar till ekvationen f (x) = x kallas jämviktslösningar till det dynamiska systemet. De kan vara antingen stabila eller instabila. Löst uttryckt är ett jämviktsläge stabilt om systemet närmar sig det för startvärden som ligger nära det, medan det är instabilt då lösningarna försvinner iväg från det, oavsett hur nära vi startar. Exempel Om b > 1 har vi i föregående övning två skärningar mellan de två graferna, x = 0 och x = b − 1 i första kvadranten. Av dessa är x = 0 instabilt medan x = b − 1 är stabilt. Om emellertid b ≤ 1 finns det bara ett jämviktsläge, x = 0, och detta är då stabilt. Det är innebörden av analysen i övningen. Övning Betrakta nu det dynamiska system som utgår ifrån funktionen bx2 f (x) = . 1 + x2 Undersök hur många jämviktslägen det finns i första kvadranten för olika b och avgör vilka som stabila och vilka som är instabila. Om vi tänker oss att an i motsvarande dynamiska system utgör en djurpopulation, förklara påståendet att om a0 är mindre än ett kritiskt värde ac kommer populationen att dö ut, medan om det är större kommer den att nå ett stabilt jämviktsantal. för olika r > 2. Ta det som en laborativ matematisk undersökning att ta reda på vilka stabila jämviktslägen som finns för olika r. Men var försiktig, öka r i små steg! Det du ska finna är att det för 2 < r < 2.570 . . . finns periodiska lösningar på systemet, med en period som växer med r (experimentera så att du förstår vad detta betyder). Men när du passerar det övre värdet inträffar något som kommit att kallas kaos. Men det är en annan historia....